Cooling by adiabatic demagnetization
As seen from the picture, at any constant temperature, a magnetized sample has lower entropy than an unmagnetized one (see entropy, an intuitive approach). This is because in the presence of an external magnetic field, parallel states have not anymore the same energy as antiparallel oriented states. The particles tend to accumulate at the lower energy state, the orientation is not random anymore, and hence entropy is lowered.
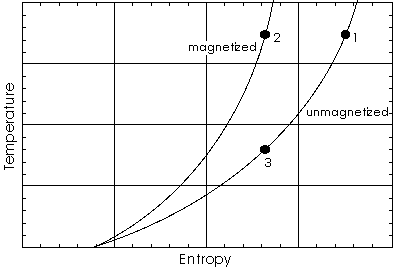
A temperature versus entropy diagram of the adiabatic demagnetization process. Two lines show how temperature varies with entropy; the upper line is for a magnetized sample, the lower one for the same sample but unmagnetized. Cooling by adiabatic demagnetizing goes like this: a sample at state (1) is magnetized in thermal contact with a heat bath. While its temperature stays constant, the entropy is lowered and the heat dQ = TdS is released to the heat bath. This process ends at state (2).
Then the system is isolated and the magnetic field slowly reduced to zero. The overall entropy of the system is constant because of dQ = 0. Because the system has to move to the lower curve describing its unmagnetized state, it is evident that temperature has to go down. How can this be interpreted from statistical mechanics?
Statistical mechanical interpretation
In our two-level-model there are only two magnetic states: either the "elementary magnets", out of which the material is made of, are oriented parallel to the field, or they are antiparallel to it. In the first case the north pole of the elementary magnets are oriented towards the north pole of the external field. This is not anymore a stable position, as soon as the field is switched on. Hence the magnets tend to flip around so that their north pole faces towards the south pole of the external field, therby losing energy. When most of the tiny magnets are parallel to each other (and antiparallel to the external field), the material is obviously more ordered and therefore has its entropy lowered.
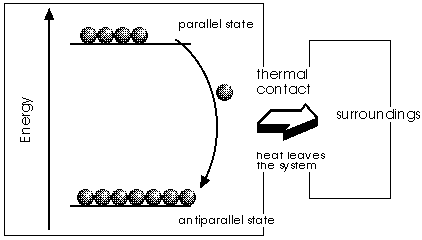
The image shows a system when the external magnetic field is on. Under these circumstances, the two possible heading of elementary magnets have not anymore the same energy and the particles tend to accumulate in the state with lower energy content. Parallel and antiparallel is with respect to the external field. Because at this stage the system is kept in a heat bath (isothermal step), the energy released by the flipping particles is transferred out of the system into the heat bath. Think of this flipping, which is taking place in a strong field, as a vigorous motion that kicks neighbouring molecules to violent vibrations. The molecules are getting energy from the magnets that they cannot give back to them, because the magnets, held in place by the external field, are acting like springs: they bounce back each impacting molecule, leaving it with the energy it had before.
When the magnetic field is removed, the spin states get randomly oriented again. The entropy of the spin states increases again.
But the demagnetization step occurs at constant entropy: if the demagnetization is done very slowly, so that no turbulence would shuffle the molecules, no entropy is generated. And, in this stage, the system is isolated such that no heat, and thus no entropy penetrates into it.
It follows that, if the entropy of the overall system is constant and the entropy of the spin states is increased, this increase must be offset by a decrease of entropy somewhere else in the system. This occurs in the thermal motions of the molecules. Hence the entropy of the thermal motion decreases, and for this to happen, the thermal motion itself must decrease. But this means lower temperature.
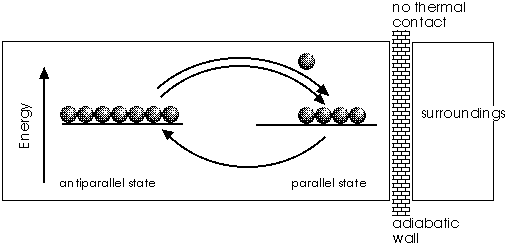
The picture shows the situation without external field; the energy levels of the two magnetic states are equal. Thus nothing prevents the elementary magnets from scattering over all possible states (only two are considered here). They are randomly kicked by the thermal motions of the atoms from one state to the other and vice versa. The probability of getting from state (p) to state (a) is proportional to the number of magnets in that state, and so it is for the reverse process. For the depicted case it is more probable that a particle goes from antiparallel to parallel. In equilibrium, both states are equally populated. Now the molecules, that got energy from the magnets in the isothermal step, can give it back to them. The magnets do not act as "springs" in this case, because they are slack. Instead of throwing back molecules on impact as before, they take up their energy and do not reflect it. So heat is now transferred back from the molecules to the magnets (of coursen, it does not stay there for ever, but is equilibrated out eventuelly with the motional energy of all the molecules. On the average, they contain more kinetic energy). Overall, the magnets act as a heat pump.
back to article,
Last update Mittwoch, 8. April 2009