Articles at the Maxwellian Demon site

Entropy? An intuitive approach by Gian Vasta

In this article I try to introduce a non-statistical concept of entropy, strictly following the thermodynamical definition. Entropy is presented as a fundamental term necessary to the definitions of heat, temperature, work. Examples that you can (and should!) work through help giving you a feeling of how entropy behaves in some basic processes. The statistical interpretation is roughly sketched in one of the examples. Finally, some applications of entropy with respect to phase transitions and the growing of living beings are scetched.

Entropy? A scientific approach by Gian Vasta

In this section, a bunch of articles are given in loose order, that step further into some of the concepts developed in the two basic articles. This page is under construction (and will be for a long time, probably. I have many ideas... ). For the time being, there are three articles ready, one about negative absolute temperature (Nov. 97), one about measuring entropy (Dec. 1997) and, new (Jun. 1998), an examination of the term "temperature"

Gibbs' Paradox by James Baugh

How we only get finite entropy with a fundamental unit of action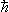

. How, classically, entropy of ensembles of particles doesn't add up when combining ensembles (Gibbs' Paradox) and how this is overcome by not counting indistinguishable particles as distinguishable. First draft (April 1998).

Information and Probability Distributions by Marijke van Gans

A three-part introduction to classical information theory, from probability distributions (April-June 1998).
Information: the concept is an introduction to the concept of information as used in science, from coin tossing and playing card examples. Where do those logarithms come from? With 2 problems.
Information in discrete distributions finally uploaded in near-final form (10 June).
Information in continuous distributions to follow.