With the coming of the computer age we are all familiar with expressing the
size of memory chips and files on disk in bytes, kilobytes, megabytes...The first in a sequence of introductory articles
on information and probability distributions
version of 98-06-10
by Marijke van Gans
| here | Information in discrete distributions >
Our everyday use of the word, and our intuition that there is such a thing as information, may both be helpful and distracting in understanding what mathematicians and physicists mean when they use the term.
Helpful, because we appreciate that information is a quantitative concept (the combined telephone directories of a whole country contain more information than that for a single one of its cities). Because it gives us a notion of information as an additive concept (the telephone directories for the separate regions together form the whole stack). And because it makes us familiar with the idea that information can be stored and can be transmitted.
Distracting, because the everyday use of the term has all sorts of associations with knowledge, useful information, meaningful information. But just like other words such as energy, force, heat, acceleration, when hijacked by science, the term information too acquired a specialised meaning that is both narrower and wider than the everyday one. Some of the most important differences:
With the coming of the computer age we are all familiar with expressing the
size of memory chips and files on disk in bytes, kilobytes, megabytes...
If we were doing an experiment tossing a coin many many times, we could record the outcomes on a computer, one bit for each toss (say 0 for heads and 1 for tails). Eight bits fill a byte, 1024 bytes in a kilobyte, 1024 K in a megabyte, 1024 meg in a gigabyte, and so on.
Some other situations also map well to the two-way choices digital computers employ for their data storage. DNA is a prime example, the choice between A, G, C, T (adenine, guanine, cytosine and thymine based nucleotides) is two bits. This way, your complete genome (diploid) is 1.5 gigabyte, about two CD-ROMs.
For obvious reasons, examples in probability theory are often taken from games involving dice or cards. Many card games use only the 32 cards higher than the six, that is 7,8,9,10,J,Q,K,A from each of four so-called "suits", clubs, diamonds, spades, and hearts. The identity of one card can be expressed as the answers to exactly 5 yes/no questions.
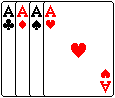Two questions to find out the suit:
1) A red suit? (if no, it's black)
if yes, 2) Hearts? (else it's Diamonds)
if no, 2) Spades? (else it's Clubs)
Three more questions decide on the "value" of the card:
3) Is it a numbered card? (counting Ace not as a number)
if yes, 4) Is the number even?
if no, 4) Is it a male figure? (yes for Jack and King)
5) at this stage there are only two possibilities left, 7 & 9, or
8 & 10, or J & K, or Q & A (and we know the suit). So the fifth
question can be put in a form to resolve which of the two it is.
This is straightforward binary of course. The 32 cards are given each a 5-bit number, and the 5 questions refer to each of the individual 5 bits.
In the card example, we can separate the suit information (two questions) from the information what "value" the card has (three questions to distinguish 7,8,9,10,J,Q,K,A). Here 2 bits of suit info plus 3 bits of "value" info gives 5 bits overall. Now it may not come as a world shattering revelation that
2 + 3 = 5
But there is actually a subtle point here. The suit info distinguishes between four cases, and the value info between eight cases. And obviously, 4 plus 8 is not 32, rather, 4 times 8 is 32, the total number of cases.
4 * 8 = 32
So the amount of information, and the number of (equally likely) cases this information distinguishes between, are related in a special way. A way that turns multiplication of numbers of cases into addition of amount of information. Such a relation is logarithmic, and because bits are about two-way choices we've effectively been using the 2-based log.
2 cases: 1 bit, as ²log 2 = 1
4 cases: 2 bit, as ²log 4 = 2
8 cases: 3 bit, as ²log 8 = 3
16 cases: 4 bit, as ²log 16 = 4
32 cases: 5 bit, as ²log 32 = 5
What's the deeper significance of using logarithms? What is the difference between the statements
a) This amount of information is enough to distinguish between 32
equally likely cases
b) This amount of information is exactly 5 bits
Well, there's no difference. The statements are exactly identical. The only reason we use logarithms is precisely because
Note that "combined system" and "composed of" are not well defined at this point. Considering any physical system as composed of subsystems is a tricky business. Just like some energy may be associated with how the parts of a whole are arranged together, the same can be true for information.
So far we've only looked at situations where there are choices between two outcomes (or a nice power of two), and the outcomes being all equally likely. We will need to look beyond these restrictions.
One question that arises is what happens with other numbers. The answer is that we can still take the ²log, but that we don't get nice whole numbers. For instance, a choice between 10 equally likely outcomes contains ²log 10 = 3.322... bits.
We need not use ²log's, we could have used log's to any other base. The important thing to remember is that a change of base multiplies the values of all our log's by the same amount. For instance, changing from base 2 to base 16 would make all values 4 times as small. A change from base 2 to base 10 would make all values 3.322... times as small. So a change of base to measure amounts of information is exactly analogous to a change from, say, centimeters to inches to measure length: a change of units.
In fact, in information theory and in physics we use base e for our logarithms, the "natural" logarithm, because this simplifies lots of expressions, especially those involving differentiation: the derivative of log x is 1/x whereas the derivative for log's to any other base is (some constant)/x. This means one "bit" is now (log 2)/(log e) = 0.693... "natural" units.
Another question that arises is what happens with choices between outcomes that are not equally likely (and even situations where the outcome of one choice affects probabilities for outcomes of a subsequent choice). This is tied up with the concept of redundancy, which is addressed in the next article. The best way to appreciate what's ahead is to try and do the following two puzzles i've prepared for you...
Coding theory is a branch of applied information theory that deals with
messages, which are a linear string of symbols. The area of
application is quite wide, for instance such symbols can be
> the letters and punctuation of written English
> the phonemes of spoken English, or any other language
> the dots, dashes and spaces of Morse code
There are many situations which we wouldn't usually consider transmission of
messages, but as the same mathematical ideas can be applied to them these too
are referred to as symbols and messages in information theory:
> a record of coin tosses can be called a message with symbols HEADS and TAILS
> a record of die throws can be called a message with symbols 1,2,3,4,5,6
> any computer file can be called a message with symbols 0 and 1
> a series of physical measurements an be called a message
and so on. Information theory was developed originally to deal with practical
communications issues, such as bandwidth in telephone systems, and therefore
communications based terminology abounds in information theory as a whole.
Now imagine a language that contains just 4 symbols:
O + < >
There are no spaces or punctuation other than these characters (imagine the + is a kind of space, the O a vowel, and the others consonants, if you want).
Problem 1: Think up a binary code for this alphabet.
Rules of the game: the computer storage medium has only 0's and
1's. That is, not 0's and 1's and some grouping
character, not 0's and 1's and a space, etc. In other
words: an unbroken string of zeroes and ones must convey the message.
You do not have to worry about a message being picked up in mid-stream,
it's enough just to be able to tell where one letter ends and the next one starts when a message
is read from the beginning.
And finally, you don't have to worry about marking the end of a message
(imagine the message files come with a directory telling the size of each
message).
Problem 2: Now we are given that the frequency of characters in this
language is
O 50%
+ 25%
< 12.5%
> 12.5%
Can you now think up a better binary code? Better here means that we want
the messages, in binary, to take up the least possible amount of storage space,
on average.
Rules of the game: the same as before.
When choosing between equally likely outcomes, say T of them (for simplicity, think of T as a power of two for the moment), we saw that the amount of information needed to specify a choice is ²log T bits. But we can rephrase that. In this situation, each outcome has a probability of 1/T. So we could just as well say the amount of information is -²log(1/T) bits, or in general -²log p bits, where p is the probability of each outcome. Cf. the first puzzle, where each outcome had a probability of 1/2² and was encoded in 2 bits.
We are now in the position to deal with the more general situation, where the outcomes can have unequal probabilities. If one particular outcome, say the ith one, has probability pi we could say that recording this outcome needs -²log pi bits. And that's exactly what we did in the second puzzle, where outcomes with probabilities of 1/2¹, 1/2² and 1/2³ were encoded in 1, 2, and 3 bits respectively.
This is the shape of things to come. But before embracing expressions like -log pi into our formulæ, we will need to take a step back and ask ourselves what it means to talk about information as a quantitative concept, and explore more fully why and how probabilities are used to define it. The next article in this series aims to do this, for discrete probability distributions.
| here | Information in discrete distributions >
Originally written April '98 and edited/extended since, most recently 98-06-10,
by Marijke van Gans
marijke@maxwellian.demon.co.uk