How temperature can be defined
independently of any thermometric substance

The Carnot cycle

1. between intersections A and B: isothermal expansion at high temperature;
   the heat Q_hi is transferred to the engine and the work -W₁ is done by the engine
2. between intersections B and C (out of the diagram): adiabatic expansion to low temperature;
   no heat is transferred; the work -W₂ is done by the engine
3. between intersections C (out of diagram) and D: isothermal compression at low temperature;
   the heat Q_lo is transferred from the engine and the work W₃ is done on the engine
4. between intersections D and A: adiabatic compression to high temperature;
   no heat is transferred; the work W₄ is done on the engine

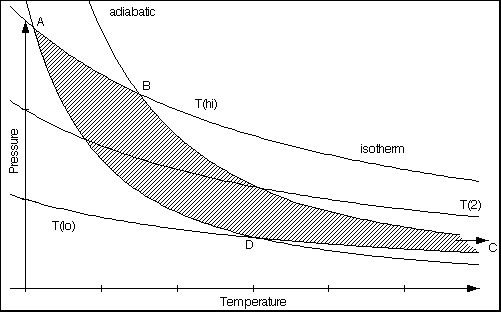
Fig. 1
A p/v-diagram shows three isotherms and two adiabatics intersecting them. The intersection points are A, B, C, D; C is out of the diagram. A Carnot process may cycle through these four points. The dashed area is the work released by the process during one cycle.

Why cyclic? Well, if it isn't then the process causes additional changes in the surroundings. Look at these processes:

• Heat flowing spontaneously, any other change excluded, from a cold body to a hot one, thus causing the hot body to become hotter at the expense of the cold one, would be a miraculous event
• Heat flow from a cold (liquid) body to its surroundings, such that the cold body cools down spontaneously, is quite common if this heat flow is caused by evaporation of the liquid. The evaporation is an additional change that drives the heat flow opposite to the temperature gradient
• The spontaneous ordering of a deck of cards would be quite a fluke
• The spontaneous ordering of freezing water molecules is ordinary because it is accompanied by an enormous release of heat to the surroundings.

None of these processes can be reversed at the same conditions; the changes they cause are permanent. However, a heat engine should not cause permanent changes; all permanent changes of the process of converting heat into work are ascribed to the heat flow from the source to the sink, which are not part of the engine. Thus the process in the engine itself must be cyclic. This also helps in using the engine over and over <g>

Efficiency of heat engines

= -w/q,

where -w is the work the engine outputs (this is why it is negative), and qq is the heat input. Thus we have

w = W1 + W2 + W3 + W4

q = Qhi + Qlo

Qhi > 0

at high temperature and outputs the heat

Qlo < 0

at low temperature. In the two expansion phases it outputs work into its surroundings

W1 < 0; W2 < 0

and in the compression phases work is done upon the engine

W3 > 0; W4 > 0

Total energy must be conserved (just another empirical law <g>) so

dU = 0 = q + w

It follows that

q = -w

and

Qhi + Qlo = -w

By definition

= -w/q = (Qhi + Qlo)/Qhi (eqn. 1)

This is the maximum possible efficiency of a heat engine; if there was a more efficient heat engine, say one based on a different working substance, then one could build an engine that does nothing but convert heat into work and that is (empirically!) impossible. It follows that the formula gives the maximum efficiency independend of the working substance.

How to use the efficiency of the Carnot process
to define temperature

The efficiency of a Carnot cycle is a funcion of the two working temperatures (_hi, _lo are empirical temperatures) of the hot and cold heat reservoirs alone

= g (hi, lo)

(and we know that g (hi, lo) = Qhi/Qlo)

hence Qhi/Qlo must also be a funcion of the two temperatures alone

Qhi/Qlo = f(hi, lo),

since

(Qhi + Qlo)/Qhi = 1 + Qhi/Qlo = g = f + 1

Consider two Carnot cycles on top of each other (see fig 1), sharing an isotherm at ₂, where the first process cycles between _hi and ₂ (with heats involved Qhi and Q2, respectively) and the second at 2, lo (heats Q2, Qlo). ₂ is between (hi, lo). Of course you can look at these processes as being one single process between (hi, lo) with heats involved (Qhi, Qlo). Then

Qhi/Q2 = f (hi, 2)
Q2/Qlo = f (2, lo)
Qhi/Qlo = f (hi, lo)

By multiplying the first equation with the second you get the third, hence

f (hi, 2) * f(2, lo) = f(hi, lo)

It is easy to see that this holds if

f(hi, lo) = F(hi) / F(lo)

(and respectively for the other f's) where F denotes an arbitrary function of one variable (substitute the ratio of the capital F's for each f(_hi, _lo) and you will see!). It is probably much less easy to show that this is the only choice, but let us leave this to the mathematicians and trust them when they assert it is so. It follows that

Qhi/Qlo = F(_hi) /F(_lo)

It was Kelvin who used this equation to define a thermodynamic temperature, independend af any specific thermometric substance. Of course he put it the simplest way by defining F() = T. From this follows

Qhi/Qlo = Thi/Tlo
or Qhi/Thi = Qlo/Tlo
or Q/T = constant

for a reversible Carnot process. The effectivity (eqn. 1) thus becomes

= 1 - Tlo/Thi (eqn. 2)

The Kelvin Temperature is equal to the Absolute Temperature
as defined by the expansivity of an Ideal Gas

If the working substance in the cylinder is an ideal gas, which is mathematically defined by

pV = nRT,
pressure times volume equals (number of moles) times (universal gas constant) times temperature,

For a isothermal expansion of an ideal gas we have:

dW = pdV = RTdV/V = dQ, (eqn. 3)

the latter equality being valid because for an isothermal expansion of an ideal gas dU = 0. On integration

Q = RT ln (V2/V1)

Thus we have, respectively:

Qhi = RThi ln (VB/VA)
Qlo = RTlo ln (VD/VC)

(please refer to fig 1. for the identifiers). Put this into equation 1 to get:

Tlo * ln (VD/VC)
= __________________ + 1
Thi * ln (VB/VA)

It can be shown that

VB/VA = VD/VC

so that:

= 1 - Tlo/Thi

This is the same result as in equation 2, hence the two temperatures must be identical.

back to article