What is Temperature?

You can always take readings of a measuring device like a thermometer. But they don't always have any meaning. How to make sure they do, and how theory can help achieving this very practical aim is discussed in the following. Temperature does not depend on how it is measured, but not every quantity shares this property; what are the conditions for physical quantities to be independend on the observer and the specific procedures she prefers? What is temperature and why can we be confident that it is a real property of systems?

The laws of thermodynamics are rather chary of temperature; the Zeroth Law merely states:

there is a quantity that is equal among bodies at thermal equilibrium.

Temperature is an equilibrium quantity

Let us see what can be learnt from this. First, temperature can only be meaningfully defined, if there is thermal equilibrium between the thermometer and the body the temperature of which is to be measured. This is the reason why meteorologists always give temperature in the shadow. It is simply impossible to state exactly, what meaning the reading has if taken in the sun.

This is more than nitpicking pedantry but also important in practice, since you expect several readings of the same thermometer to give the same number and, even more, several thermometers to give the same temperature. If there is no equilibrium between thermometer and the body, thermodynamics says that you cannot expect these statements to be valid and hence, the meaning of the term "temperature" is questionnable.

The reading of a thermometer shone at by the sun gives more or less the temperature of the thermometer itself - but this is usually not what you want to know. This temperature is the result of a dynamic equilibrium: a certain amount heat Q₁ flows from the sun (heat source) to the thermometer and an other amount Q₂ from the thermometer to the air (heat sink); if the heats are different, the temperature of the thermometer changes. For instance, the thermometer gets hotter if Q₁ is larger than Q₂ and it gets cooler if Q₂ is larger. But Q₂, among others, increases with increasing temperature of the thermometer. Thus, at given Q₁, eventually both heat flows become equal, and a dynamic equilibrium is reached. Unfortunately, this temperature has nothing to do with the temperature of the surrounding air.

On the other hand, if the thermometer is placed in the shadow, the sun as a heat source to the thermometer is removed and a (static) equilibrium between thermometer and air can be attained eventually. That is, the heat source and the heat sink are identical in this case. Then each thermometer measures the temperature of the air, and if appropriately calibrated, gives the same reading.

If you want your thermometer reading to mean more than the figures that show up when throwing dice, you have to carefully determine

if there is equilibrium
what kind of equilibrium it is (heat source and heat sink have to be identical)
which bodies are in equilibrium

In short: you can always take readings of a thermometer, but they do not always make sense; it is your responsibility to make sure they do. By the way: this applies to every kind of measurement.

Didn't imagine measurement of temperature being that intricate, huh?

Measuring temperature

Everybody knows how to measure temperature: take a thermometer and stick it into whatever you want to know the temperature of, wait a little bit and get the reading. You even know now why you have to wait that little bit, don't you? An instance of incertainty might arise if there is no hole to stick the thermometer into, but let us leave that open for the moment, and have a closer look at the thermometer itself. They come in a large variety, some are glass tubes filled with liquid (coloured alcohol) or even with mercury. There are these bimetal thermometers and the ones with the LCD display. Each of them determines a different property of matter that changes with temperature, and they are all supposed to give the same reading when in equilibrium with the same heat bath. Do they really do this?

Of course they don't.

So does this mean that temperature depends on what substance you take and what property you choose to determine it? Yes and no:

No - the temperature itself does not depend on the thermometric substance. It must not, if temperature is to mean more than just a heuristic concept.

Yes - in the sense that the reading of temperature depends on the method you use to get it. This means that a thermometer only gives an estimation of temperature which may be biased depending on what method you use. Hence, for accurate measurements, any thermometric device has to be calibrated with the thermodynamic temperature scale.

Temperature of a solid

What do you do if there is no hole to stick the thermometer into? As stated, one condition for temperature readings to mean anything is thermal equilibrium between body and thermometer. This is not easy to achieve at the surface of a body, and that is where a hole may help. Additionally, one has to make sure that there is thermal equilibrium within the body itself. Remember that without this condition you can get readings of a thermometer, but don't expect them to be reproducible. If three successive readings of a thermometer at the surface of an aluminium block were 38, 52 and 43 °C what would you expect its temperature to be? If you are tempted to take the algebraic mean, remember that although you can always calculate the mean of a bunch of numbers, it does not always represent something real. For instance, you could even take the mean of the phone numbers of your friends, but you would not expect to get them all with a single call by dialing that number (even if you could figure out how to manage the decimal places <g>). At least, some means (but not that of the phone numbers) may represent some population, think e.g. of the hights of your friends. In the case of the measurement of a physical quantity, we usually want more than just a population mean. We want the mean to represent the true value.

Temperature does not depend on thermometric substance

Between 1802 and 1808 Joseph Gay-Lussac investigated the volume change of gases by heating, and found that in the limit of zero pressure all gases had the same thermal expansivity.

V = V₀ * (1 + *)

where

V is the volume of a gas at temperature ,
its thermal expansivity,
V₀ the volume at some arbitrary chosen reference temperature and
the temperature as measured at an arbitrary scale

If temperature is measured in the Celsius scale, the expansivity, independend of material used, amounts to

= 1/273,

From this, it appears convenient to define a new temperature scale such that

T = + T₀.

The above stated law of Gay-Lussac then becomes

V_T = V₀ * (1 + (T - T₀)/T₀

V_T = V₀*T / T₀

In this new scale there are no negative temperatures (though, negative Kelvin temperature is not meaningless in some special systems, see "Is there negative Kelvin temperature?"); it is the Kelvin scale. It was Kelvin who used the Second Law of thermodynamics to define a thermodynamic temperature scale, which is completely independend of any thermometric substance. His temperature scale does not refer to, but complies with, the results of the studies of Gay-Lussac. In fact, the method of Gay-Lussac provides a means to determine directly the thermodynamic temperature.

He could do this after the efficiency of a carnot cycle has been discovered to depend only on the temperature of the heat source and the one of the heat sink (Sadi Carnot, 1824). If this holds, temperature can be defined as the quantity that determines the efficiency of a Carnot cycle. A closer look at the Carnot cycle reveals that its efficiency is the maximum work you can get out of a given amount of heat. Remember the definitions of heat and work:

work: energy transferred at constant entropy between systems
heat: energy transferred between systems accompanied by entropy change,

then you can guess that the energy loss must be due to entropy, and in fact, as shown in the next paragraph, temperature will turn out as describing how energy changes when entropy changes.

Temperature and the laws of thermodynamic

It has been stated before what the Zeroth Law says about temperature. The law did not have to be more precise, because everything else that had to be said on temperature has been stated in the other laws. Hence, if you want to know more quantitatively what temperature is, you have to refer to the other laws, too.

The First Law is the well-known energy conservation law. It states that every change of internal energy of a system must be due to energy transferred to it from the outside. Energy can be transferred to or from a system as heat or as work.

dU
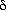 = Q
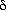 + W

(eqn. 1)

where

dU is infinitesimal change of internal energy
Q is infinitesimal amount of energy transferred as heat
W is infinitesimal amount of energy transferred as work
hints at the fact that neither work nor heat are total differentials

Energy is transferred as work, if a process does not change the entropy of the system, and it is transferred as heat, if entropy of the system is changed. These statements define heat and work, respectively.

The Second Law comes in two flavours:

the first states that no cyclic process is possible that does nothing but convert heat into work (the Kelvin statement)
the second states that no cyclic process is possible that does nothing but transfer heat from a cold body to a hot one (the Clausius statement)

Of course the two "flavours" are one; they are logically equivalent. The Kelvin statement is related to the efficiency of a Carnot cycle: it denies the existence of a heat engine with efficiency equal to unity. We have seen before (in the note about the carnot cycle) that this leads to the conclusion that, for a reversible Carnot process,

Q/T = constant or
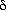Q/T = 0

Thus for reversible processes Q/T is conserved. Mathematically, it is a total differential, called the entropy dS. Hence, for reversible processes, total entropy is conserved,

dS = 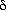Q_rev/T

If the process is not reversible, the heat engine loses energy by friction, hence

Q_hi/T_hi > Q_lo/T_lo

Q_hi/T_hi - Q_lo/T_lo > 0

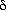Q/T > 0

dS > 0

To put this bunch of formulas into words:

because of losses the engine must take up even more heat than it does without losses
because of losses, entropy gets larger
to keep entropy conserved, a minimum loss, the heat dumped to the cold sink, is needed (this is the Kelvin statement of the Second Law)
if a given amount of heat is released to a cold bath, its entropy is raised more than if the same heat is released to a hot bath (the Clausius statement of the Second Law)

So finally, we recognize the equation

dS = 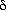Q_rev/T (eqn. 2)

as the Second Law.

Combining First and Second Law

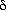From the Second Law (eqn. 2): Q = TdS (for reversible processes). Put this into the First Law (eqn. 1) to get:

dU = TdS - pdV,

where we are considering only PV work. Since the internal energy U is a total differential:

dU =

+

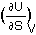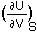
Thus by comparison:

T = ;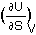

- p =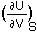

This can serve as the definition of temperature we have been looking for. Let us see how it works.

If a given amount of heat is transferred to a system then its iternal energy is rised, and so does its entropy. This is depicted in the following diagram

Picture 1The image shows how internal energy changes upon increase of entropy; if this suggests to you that it must be possible to take control of the entropy of a system, then you are on the right path. Keep in mind that the changes in the system we are discussing here are caused by the addition of heat, and this, by definition, is the transfer of energy while changing entropy. Thus, by heating or cooling (among other), you can control the entropy of a system.

In this picture, the slope at a given entropy indicates how much the internal energy goes up for an infinitesimal change of entropy. This ratio is the temperature. Thus, from the First and Second Law combined it follows that

temperature is the ratio of internal energy (U) change by entropy (S) change,
T =

The diagram indicates that at high entropy, the slope is steeper than at low entropy. That means, since the slope is temperature, that temperature goes up from the left to the right. This corresponds to the fact that at high temperature, adding a given amount of heat to a system, raises its entropy less than does the same amount of heat at a low temperature. As worked out in the "historical approach to entropy"article (not yet available), this is essential to make heat engines work.

As an exercise, you may try to figure out how this diagram looks like for a system undergoing a phase transition. To be specific, imagine a pot of boiling water. In spite of heating, temperature stays constant, but the water changes its phase from liquid to gaseous. What would the diagram look like? Click here for a solution

Last update Mittwoch, 8. April 2009